Distância entre dois pontos

A base da geometria analítica encontra-se na distância entre dois pontos, pois muitos conceitos são inerentes a esse. Portanto, compreender a expressão algébrica para o cálculo da distância entre dois pontos colabora para uma compreensão fidedigna de outros conceitos da geometria analítica.

Dado o plano cartesiano, vamos estabelecer a distância entre os pontos A e B.

Podemos observar que os pontos possuem coordenadas, sendo o ponto A (xa,ya) e B (xb,yb), note a formação do triângulo retângulo ABC, onde os lados BC: cateto, AC: cateto e AB: hipotenusa.
Verificamos que a distância entre os pontos A e B é a hipotenusa do triângulo retângulo, que pode ser calculada aplicando o Teorema de Pitágoras. Com o auxílio da Álgebra e de conhecimentos geométricos podemos generalizar e construir uma fórmula que determine a distância entre dois pontos no plano, conhecendo suas coordenadas.

Cateto BC: yb – ya
Cateto AC: xb – xa
Hipotenusa AB: distância (D)

Pelo Teorema de Pitágoras temos: “o quadrado da hipotenusa é igual à soma dos quadrados dos catetos”

Note que basta fazer as diferenças das coordenadas de cada um dos pontos e elevar ao quadrado, contudo são coordenadas do eixo X com coordenadas do eixo X e de forma análoga para as coordenadas do eixo Y.

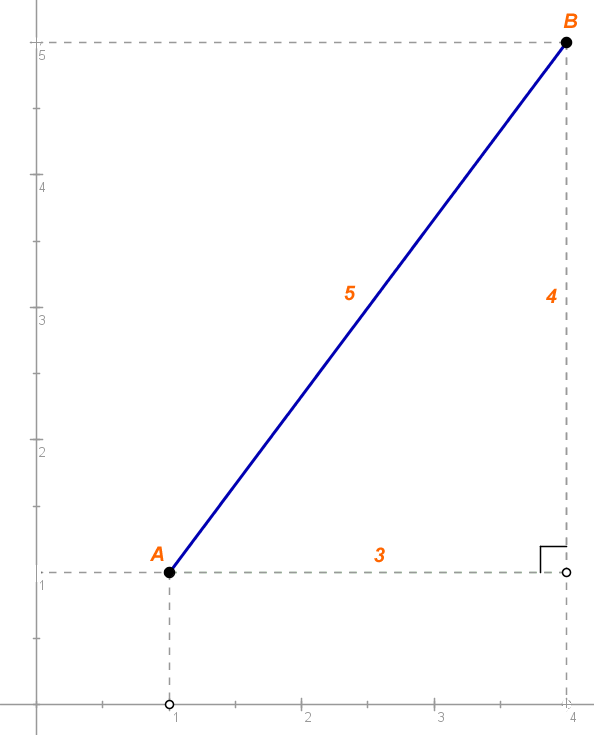
Calcule a distância entre os pontos: A (4,5) e B(1,1) e represente-os geometricamente.
Como vimos anteriormente, basta aplicar a expressão para o cálculo da distância entre dois pontos. Sendo assim:





Geometricamente:

Fonte:

 http://www.mundoeducacao.com/matematica/distancia-entre-dois-pontos.htm

Formula da distância entre dois pontos

Podemos determinar uma expressão que indica a distância entre A e B, quaisquer que sejam  A(X1, Y1) e B ( X2,Y2).

O triângulo ABC é retângulo em C, logo podemos usar a relação de Pitágoras:

Concluímos então, que a distância entre dois pontos A e B quaisquer do plano, tal que A(X1,Y1) e B(X2,Y2), é  dada por: 

Exemplos: 

Um ponto P (a,2) é equidistante dos pontos A(3,1) e B (2,4). Vamos calcular a abscissa do ponto P.

Como P é equidistante de A e B, devemos ter:

d(P,A) = d(P,B)   →→

(3-a)² + 1= (2-a)² + 4 → 9-6a+ a² + 1= 4-4a+ a² + 4 → -6a +4a= 4+4-9-1 → -2a= -2→ 2a= 2→  a= 1

Então, a abscissa do ponto P é 1.

Observação: É útil notar que duas distâncias entre dois pontos são iguais se, e somente se, seus quadrados também o são. Portanto, muitas vezes, a extração da raiz quadrada é desnecessária.

Nesse exemplo, poderíamos ter iniciado assim:

d(P,A) = d(P,A) → [d(P,A)]² = [d(P,B)]²  → (3-a)²  + 1= (2-a)² + 4 → 9- 6a + a² +1 = 4- 4a + a² + 4 → -2a = -2 →  a = 1

Fonte: Matemática

Contexto & Aplicações

Livro - Dante volume 3;